Growth curve analysis of body weight in crossbred dairy cattle in central Ethiopia

Molla Shumye

Ethiopian Institute of Agricultural Research, Holeta Research Center, P O Box 31, Holeta, Ethiopia
mollabrkt@gmail.com

Abstract

The study was carried out to evaluate the growth curves and their parameters, as well as, to determine the appropriate non-linear growth model that best describes growth curves of various genetic groups of crossbred female calves. The study incorporated a total of 9032 body weight records taken across different months from birth up to 735 days of age on 391 (287 F₁ Frisian X Boran and 104 F₁ Jersey X Boran) crossbred female calves born at Holetta Agricultural Research Center between 1978 and 2003. The growth was fitted using nonlinear growth models such as Logistic, Gompertz, and Von Bertalanffy. Coefficient of determination (R²), Root Mean Square Error (RMSE) and corrected Akaike’s information criteria (AICc) were used to determine the best fit model in describing the growth pattern of crossbred growing female calves. The value of growth parameters (A, B, K) for all crossbred female calves from Von Bertalanffy model were 353±29.0, 0.54±0.01 and 0.002±0.0002, respectively. R², RMSE and AICc were 0.99, 4.76 and 145, respectively. Von Bertalanffy model was found to best describe body weights of crossbred growing female calves due to the lowest values of RMSE and AIC_c, as well as highest value of R ².

Keywords: Boran crosses, female calves, growth parameter, live weight, nonlinear model

Introduction

Though many definitions are given to the term growth, the simplest definition common in animal science is an increase in tissue mass (Owen et al 1993). Basically, growth occurs by two biologically interacting process: hyperplasia and hypertrophy. Hyperplasia is the process of cell multiplication and skeletal growth that mostly occur during the early stage of life, starting from embryonic stage, until mature body size is reached. The second phase of growth, hypertrophy, occurs after mature body size reached. During this period of life, growth mainly occurs by cell enlargement and incorporation of satellite cells. In either case, growth rate in farm animals involve complex processes with multiple hormones acting in concert and is influenced mainly by genotypes, environment and the interaction between the genotypes and the environment which exert their effects throughout the three phases of early growth periods: prenatal, pre-weaning and post-weaning growth (Owen et al 1993).

In Ethiopia and elsewhere, most of studies on evaluation of growth traits are focused on beef cattle since growth are the main economical traits for beef industry. But growth trait is also one of the important parts of dairy cattle goals and needs to be evaluated in any breeding program. In dairy cattle, culling can be more accurate and stocks can be replaced earlier if growth rates are better as heifers can calve at younger age and increase their lifetime productivity (Hohenboken 1985 as cited by Gizachew et al 2003).

Under the Ethiopian context, some reports (Sendros et al 2003b; Kefena et al 2006) reported relative performances and genetic parameters of the early growth traits of indigenous breeds and their crosses with regard to birth weight (BW), weaning weight (WWT), six-month weight (SMWT), yearling weight (YWT). Moreover, several attempts have been made to improve the productivity of some of the economically most important traits such as milk production and reproduction performances through crossbreeding. The results of these crossbreeding experiments in Ethiopia have been amply reported in several literatures (Beyene 1992; Sendros et al 2003a; Kefena et al 2006; Kefena et al 2011; Kefena et al 2013).

The course and growth patterns of various genetic groups of crossbred dairy growing cattle from birth to puberty age have substantial economic implication and greatly contribute to the dairy cattle genetic improvement programs. However, in Ethiopia, nearly all available evidences on crossbred dairy cattle focus on the post-calving traits such as on productive and reproductive performances. So far, no empirical evidences were available on the growth curves of early growth traits of different genetic groups of growing dairy cattle produced in Ethiopia. Therefore, the objectives of this study were:

· To evaluate the growth curves and their parameters of various genetic groups of crossbred dairy cattle.

· To determine the appropriate non-linear growth model that best describes growth curves of crossbred dairy cattle.

Material and methods

Description of the study site

The Holetta Agricultural Research Center (HARC) is located at 35 km west of Addis Ababa at 38.5°E longitude and 9.8° N latitude. It is situated at about 2400 m above sea level. The average annual rainfall is about 1200 mm and an average maximum temperature is 21.3 (18.6-24c^o). Common livestock specious reared around the study area are cattle, sheep, goat and equines.

Animal management

All calves were weighed immediately after birth and allowed to suckle their dams for the first 24 h, to obtain colostrum. Then after, the calves were taken to calf rearing pen and the colostrum feeding continued up to their 4 ^th days of age and feeding of whole milk until weaning at 98 days of age through bucket feeding method. Each calf was fed a fixed amount of 260 kg of whole milk during the pre-weaning period. Weaned calves were kept indoors until 6 months, during which they were fed ad lib on natural pasture hay and supplemented with approximately 1 kg per day per animal of concentrate composed of 30% wheat bran, 32% wheat middling, 37% noug seedcake (Guizoita abysinica) and 1% salt. All heifers above six months of age were allowed to graze on natural pasture for about 8 h during daytime. At night, all animals were housed in an open shade and supplemented with natural pasture hay. Treatment and Vaccination of the herd against common diseases were carried out by the animal health research division of the HARC.

Data source and traits considered

Repeated records of growth data were filtered from growing crossbred female calves born between 1978 and 2003 at Holeta Agricultural Research Center, central Ethiopia. Due to incomplete data records and different calf’s management systems practiced, weight data from calves born before the year 1978 and after 2003 were excluded from the analysis. One of the reasons was that F₁ Frisian X Boran (F₁FB) and F₁ Jersey X Boran (F₁JB) crossbred female calves born before and after the aforementioned years were reared by suckling their dams. The animals were weighed every month from birth to 735 days age. The initial data set consisted of 9182 weight records on 391 (287 F₁FB and 104 F₁JB) crossbred female calves. All the data were checked for correct dates of birth and weighing. Records with inconsistent dates of birth and weighing were discarded. Only records of animals with at least seven weight records were kept. The edited data set had 9032 weight records obtained on 391 animals.

Statistical analysis

Preliminary data analysis

Preliminary least squares mean analysis was carried out to test the statically difference between genetic group of crossbred cattle in growth performances over ages using general linear model of SAS (2008).

Growth curve analysis

The common growth models used were Logistic, Gompertz, and von Bertalanffy. The consideration of these three models chosen among others was based on the evident from previous studies that the three growth models are excellent for use in longitudinal quantitative data from the different types of animals and plants (Brown et al 1976; Budimulyati et al 2012).

The growth curves were fitted using nonlinear (NLIN) procedure of SAS (2008). These models were described as follow:

1) Gompertz model: Wt = A exp (-be^-kt),

2) Logistic model: Wt = A / (1+be^-kt),

3) Von Bertalanffy: Wt = A (1-be^-kt) ³

Where W_t is the observed weight at age t expressed in days, and A is the asymptotic limit of the weight when age approaches infinity mature weight, and b indicates the proportion of the asymptotic (mature weight) to be gained after birth, established by the initial values of W and t (initial weight) and k is a function of the ratio of maximum growth rate to mature weight, normally referred to as maturing rate, e Natural logarithm base and t time at when weight was observed.

Selection criteria (goodness of fit) used for assessing the best non-linear model that describe the growth curve were coefficient of determination (R²), root mean square error (RMSE) and corrected Akaike’s information criteria (AICc). Coefficient of determination (R²) was calculated using the following formula:

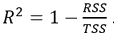TSS is total sum of squares, RSS is the residual sum of square. The R ² value is an indicator measuring the proportion of total variation about the mean of the trait explained by the growth curve model. The coefficient of determination lies always between 0 to 1, and the fit of a model is satisfactory if R² is close to unity. Root mean square error (RMSE) is a kind of generalized standard deviation and was calculated as follows-

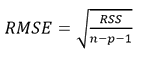Where RSS is residual sum of square, n is the number of observation (data point) and p is the number of parameters in the equation. RMSE value is one of the most important criteria to compare the suitability of used growth curve models. Therefore, the best model is the one with the lowest RMSE. Akaike’s information criterion (AIC) wereas calculated as using the equation Burnham and Anderson (2004):

AIC = n*ln(RRS) + 2p. Where ln is natural logarithm.

Corrected Akaike’s information criterion (AICc) was calculated using the equation of Motuls Christopoulos (2004):

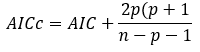AIC_c is a good static for comparison of models of different complexity because it adjusts the RSS for number of parameters in the model. A smaller numerical value of AIC_c indicates a better fit when comparing models.

Results and discussion

Preliminary data analysis

The results of preliminary least squares mean analysis which was carried out to examine the statically difference between genetic group of crossbred female calves in growth performances over their ages are presented in Table 1. Overall mean live weight of crossbred growing female calves at birth, 3, 6, 9, 12 ,15, 18, 21, and 24 months of age were 24.7, 62, 93, 113, 138, 164, 189, 216 and 245 respectively. Body weight of crossbred female calves varied high significantly (p<0.01) with genetic group. F₁FB crossbred female calves had better body weight than those of F₁JB crosses over their age points. This could be because Frisian crosses which were sired by a Frisian sire has larger body frame than Jersey sires, which has relatively small body frame (size). Similar to this finding, better growth performance of Friesian crossbred calves over Jersey crossbred calves was also been reported by Little et al (1988) and Sendros et al (1987).

Growth curve analysis

The estimated parameters of the growth curve, their standard error and goodness of fit, such as R²,RMSE and AIC_c for the Gompertz, Logistic and Von Bertalanffy models are shown in Table 2.

There were differences on the parameter estimates of the models. The A parameter that estimates mature weight was the largest for the Von Bertalanffy model for both F₁FB and F₁JB crossbred growing female calves (438 ±41.7 and 279 ±19.8 kg), respectively and the lowest for the logistic in F₁FB and F₁JB crossbred female calves (302±16.9 and 218±10.2 kg), respectively (Table 2). Similar findings of maturing body weight (A) i.e, largest for the Von Bertalanffy and lowest for the Logistic models were reported by Bahashwan et al (2015) in Dhofari cows and Koskan and Ozkaya (2014) in female Holstein calves. Different parameter estimates were reported by Salem et al (2013) in Friesian crossbred male calves, Mohd-Hafiz et al (2016) in Bali cows and Tutkan (2019) in Holstein Friesian Bulls. The difference in parameter A estimates between present result and the reports may be associated with breed and type of animals used for the studies and the environment under which the animals were managed.

The mature weight (A) of F₁FB crossbred female calves was higher compared to that of F₁JB female calves which were (438±41.7 and 279±19.8 kg) for Von Bertalanffy, (374±26.7 and 252±15.3 kg) for Gompertz and (302±16.9 and 218±10.2 kg) for logistic models, respectively. This could be due to reason that F₁FB crosses were sired by Frisian sire which has larger body frame than those F₁ JB crosses. This result is in agreement with the results of Sendros et al (1987) who reported that Friesian crossbred calves had better body weight than Jersey crossbred calves at one year of age (152 kg vs 139 kg).

The estimate for parameter k was highest for logistic model for both F₁FB and F₁JB crossbred growing female calves (0.01±0.0003 and 0.01±0.0004), respectively. Whereas, k value was found smallest and similar for Von Beralanffy and Gompertz models in both F₁FB and F₁JB crossbred growing female calves (0.002±0.0002 and 0.003±0.0002), respectively. The estimate of B parameter was highest for Logistic model in both F₁FB and F₁JB crossbred growing female calves (5.59±0.32 and 4.85±0.29) and lowest for Von Bertalanffy model (0.56±0.01 and 0.54±0.01) in both F₁ FB and F₁JB crosses, respectively.

The maturity rate (K) estimates and the integration constant (b) observed in this study did not vary greatly, compared with the result of Marinho et al (2013) who estimated K and B values of 0.01±0.00002 and 0.52±0.0008, respectively for the Von Bertalanffy model. Tutkun (2019) also obtained (0.002±0.001 and 0.74±0.01), respectively for the Von Bertalanffy model on growth of Holstein Friesian bulls. In this study, similar estimate of parameter K was also observed from three linear models for both genetic groups of crossbred female calves.

Correlation between the mature weight (A) and rate of maturing (K) was negative for all models ranging from -0.90 to -0.98 where Von Bertalanffy model provided the highest negative correlation between A and K followed by Gompertz model for both genotypic groups. The negative correlation between parameters A and k would indicate that animals with slow maturing rate attain their mature weight at later ages and are heavier. Crossbred female calves with higher maturing rate will take shorter time to attain its mature weight. The obtained result is similar to the report of (Mohd-Hafiz et al 2016; Mohd-Hafiz et al 2018) for Brakmas and Bali cows. Accordingly, animals are younger at the time of maturity than the animals with higher mature body weight.

The nonlinear models were compared using R², RMSE and AIC _c values to identify the best model in explaining the body weights of F₁FB, F₁JB and overall crossbred female calves. The highest value of R² (> 0.98) was observed for all nonlinear models used to evaluate the growth of different genetic group of crossbred female calves Table 2.

Von Bertalanffy model was found to be the best model to describe body weights of F₁FB, F₁JB and all crossbred growing female calves due to the lowest values of RMSE (4.76) and AIC_c (145), as well as highest value of R^{2 (}0.99). This is supported by Bahashwan et al (2015) results, who reported that the Von Bertalanffy model was the best to describe the growth curves of Dhofari cattle. Similarly, the Von Bertalanffy model was suggested to be the most appropriate to describe the growth pattern of Bali cows (Mohd-Hafiz et al 2016).

The different result indicated that Logistic model was more appropriate in describing growth curve of female Holstein calves (Koskan and Ozkaya 2014) and Brakmas and Bali cattle (Mohd- Hafiz et al 2018). Amrullah et al (2019) also stated that the Brody model was more appropriate in describing growth pattern of Brahaman female cattle. It showed that different datasets, breeds and environmental factors presented different goodness of fit for the models in describing body weight of cattle (Mohd-Hafiz et al 2016).

Growth curves for observed and predicted data for F₁FB and F ₁JB crossbred female calves from birth to 735 days of age are shown in Figure 1 and 2. It can be observed from the figures that all the points of curve described by each mathematical model were matching with the actual curve, except at some age facing overestimate and underestimate in predicting body weight.

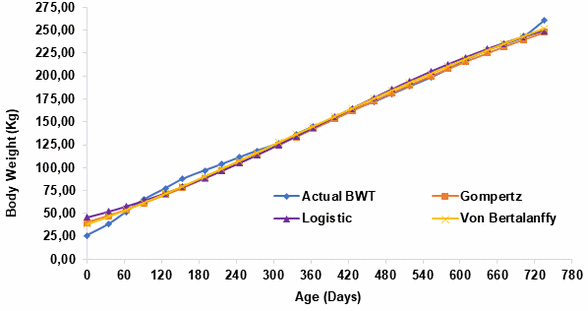Figure 1. Actual (observed) and estimated body weight (kg) as a function of age (days) in F1FB crossbred female calves with Gompertz, Logistic and Von Bertalanffy models

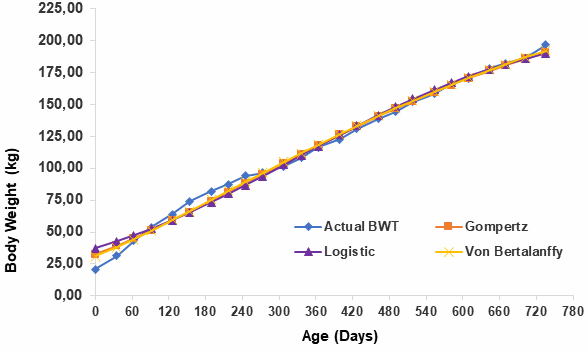Figure 2. Actual (observed) and estimated body weight (kg) as a function of age (days) in F1JB crossbred female calves with Gompertz, Logistic and Von Bertalanffy models

Von Bertalanffy model was more appropriate in predicting weight from the ages of 60 to 90 and then from 300 to 700 days of age of F₁FB and F₁JB crossbred female calves as compared to other models. All mathematical model overestimated observed body weight at birth and 30 days of age, as well as underestimated body weight observed at the ages from 120 to 240 days and at the end of test period (735 days). This result does not agree with report of Marinho et al (2013) who indicated that Von Bertalanffy model over estimate observed body weight at the age of 340 to 470 days; while in the final part of the curve, that is, starting at 670 days of age, the model underestimated the observed weights.

Koskan and Ozkaya (2014) also showed that Brody, Gompertz, Logistic, Richards and Von Bertalanffy models estimated birth weights of the calves to be low in the study conducted on the growth curves of female Holstein Calves. It indicated that body weight data of different cattle breeds managed under different environments would likely affect the suitability of nonlinear models in describing the variation in growth pattern of cattle (Mohd-Hafiz et al 2015).

The shape of the growth curve showed thatF₁FB crossbred female calves were heavier than F₁JB crossbred calves. The higher body weight of F₁FB crossbred female calves than F₁JB crosses has been described by sire body size differences between genotypes which is in agreement with the results of Little et al (1988) and Sendros et al (1987) who reported that Friesian crossbred calves had better body weight than that of Jersey crossbred calves.

Conclusion

In this study, Von Bertalanffy model was found to be the best model to describe growth pattern of F₁FB and F₁JB crossbred growing female calves due to the lowest values of root mean square error and corrected Akaike’s information criteria, as well as highest value of coefficient of determination. This study also revealed that F₁FB crossbred female calves had higher estimated mature weight compared to F₁ JB crossbred female calves. The inverse relationship between mature weight and rate of maturing indicates that animals with higher rate of maturing tend to be lighter at maturity and take shorter time to attain their mature weight.

References

Amrullah A H K, Maharani D and Widayati D T 2019 Determination of the Best Nonlinear Function in order to Estimate Brahman Female Cattle Growth in The UGM Annual Scientific Conference Life Sciences 2016, KnE Life Science. pages 122–129.

Bahashwan S, Alrawas A S, Alfadli S and Johnson E S 015 Dhofari cattle growth curve prediction by different nonlinear model functions. Livestock Research for Rural Development. 2015; 26:236. http://www.lrrd.org/lrrd27/12/baha27236.html

Beyene K 1992 Estimation of Additive and Non-additive Genetic Effects for Growth, milk Yield and Reproductive Traits of Crossbred Cattle in the wet and dry environments in Ethiopia. Ph.D. Dissertation, Cornell University, Ithaca, New York.

Brown J E, H A Fitzhugh Jr and T C Cartwright 1976 A Comparison of nonlinear models for desecribing weight-age relationship in cattle. Journal of Animal Sciences, 42:810- 818.

Budimulyati S, Noor R R, Saefuddin A and Talib C 2012 Comparison on accuracy of logistic gompertz and von Bertalanffy models in predicting growth of new born calf until first mating of Holstein Friesian heifers. Journal of Indonesian Tropical Animals Agriculture, 37(3):151-160.

Burnham K P and Anderson D R 2004 Multimodel inference: understanding AIC and BIC in model selection. Social Methods Research, 33(2), 261-304.

Gizachew B, Zelalem Y, Taddese Be, Alemu G, Sendros D, Yohannes G and Roman H 2003 Performance of two- and three-way crossbred dairy cattle at Holetta Research Center in central highlands of Ethiopia: Growth Rate. Proc. 10 ^th Annual conference of the Ethiopian Society of Animal Production (ESAP). August 22-24, 2002. Addis Ababa, Ethiopi. Pp.127.

Hohenboken W D 1985 Genetic Structure of Populations. 2. Mating Among Distantly Related Individuals. In: A.B. Chapman (Ed). World Animal Science. Elsvier Science Publisher, B.V. Amesterdam. Oxford. New York. Tokyo

Kefena E, Hegde B P and Tesfaye K. 2006 Lifetime production and reproduction performances of Bos taurus x Bos indicus crossbred cows in the central highlands of Ethiopia. Ethiopian Journal of Animal Production. 6 (2): 37-52.

Kefena E, Diriba H, Molla S and Roman H 2013 Analysis of longevity traits and lifetime productivity of crossbred dairy cows in the tropical highlands of Ethiopia. Journal of Cell and Animal Biology, 7(11), 138-143.

Kefena E, Zewdie W, Tadelle D and Aynalem H 2011 Genetic and environmental trends in the long-term dairy cattle genetic improvement programmes in the central tropical highlands of Ethiopia. Journal of Cell and Animal Biology, 5 (6). pp.96-104.

Koskan Ö and Özkaya S 2014 Determination of growth curves of female Holstein calves using five non-linear models. – Pakistan Journal of Agricultural Science, 51(1): 225-228

Little D A, Anderson F M and Durkin J W 1988 Partial Suckling of Crossbred Dairy Cows: Initial results on effects of milk off take and calf growth at Debre Berhan. In: Proc. of the 2 ^nd National Livestock Improvement Conference, 24-26 Feb. 1988, Addis Abeba, Ethiopia.

Marinho K N S, Freitas A R, Falcão A J S and Dias F E F 2013 Nonlinear models for fitting growth curves of Nellore cows reared in the Amazon Biome. – R Bras Zootec 42: 645-650.

Mohd-Hafiz A W, Mohamad Hifzan R, Izuan Bahtiar A J and Ariff O M 2015 Describing growth pattern of Brakmas cows using non-linear regression models. Malaysian Journal of Animal Science. 18(2): 37-45.

Mohd-Hafiz A W, Izuan Bahtiar A J, Mohamad Hifzan R, Ariff O M and Faezal Ashraff A L 2016 Describing Growth Pattern of Bali Cows Using Non-linear Regression Models. Malaysian Journal of Animal Science. 19(2): 1-7.

Mohd-Hafiz A W, Mohamad Hifzan R, Ariff O M, Izuan Bahtiar A J and Faezal Ashraff A L 2018 Comparison of growth pattern for body weight in Brakmas and Bali cattle using non-linear regression models. Malaysian Journal of Animal Science, 21(1): 19-28.

Motulsky H and Christopoulos A 2004 Fitting models to Biological Data using linear and nonlinear regression. Oxford University press.

Owens F N, Dubeski P and Hanson C F 1993 Factors that alter the growth and development of ruminants. Journal of Animal Science, 71, 3138-3150.

Salem M M, El-hedainy, Dalia K A, Latif M G A and Mahdy A E 2013 Comparison of non-linear growth models to describe the growth curves in fattening Friesian crossbred and buffalo male calves. Alexandria Journal of Agriculture Research, 58(3):273-277.

SAS 2008 Statistical Analysis system user’s guide, Release 9.2 SAS Institute, Inc., Carey, NC, USA.

Sendros D, Beyene K, Tesfaye K, Taye B and Hailu G M 1987 Preliminary Results of Cattle Crossbreeding (European X Zebu). studyII. Growth Performance of European X Zebucrossbred Calves In: Proc. 1 ^st National Livestock Improvement Conference. 11-13 Feb, Addis Abeba, Ethiopia. PP73-75.

Sendros D, Neser F W C and Schoemann S J 2003a Early growth performance of Bos taurus × Bos indicus cattle crosses in Ethiopia: Evaluation of different crossbreeding models. Journal of Animal Breeding and Genetics, 120:39-50.

Sendros D, Neser F W C and Schoeman S J 2003b Variance components and genetic parameters for early growth traits in a mixed population of purebred Bos indicus and crossbred cattle. Livestock Production Science, 84, 11–21.

Tutkun M 2019 Growth curve prediction of Holstein-Friesian bulls using different non-linear model functions. Applied Ecology and Environmental Research 17(2):4409-4416